一．实验目的

  1. 对于平面上给定的N个点，给出所有点对的最短距离，即，输入是平面上的N个点，输出是N点中具有最短距离的两点。

  2. 要求随机生成N个点的平面坐标，应用蛮力法编程计算出所有点对的最短距离。

  3. 要求随机生成N个点的平面坐标，应用分治法编程计算出所有点对的最短距离。

  4. 分别对N=100,1000,10000,100000，统计算法运行时间，比较理论效率与实测效率的差异，同时对蛮力法和分治法的算法效率进行分析和比较。

  5. 如果能将算法执行过程利用图形界面输出，可获加分。

二、算法原理描述

1、蛮力法

1）算法描述：已知集合S中有n个点，一共可以组成$n(n-1)/2$对点对，蛮力法就是对这$n(n-1)/2$对点对逐对进行距离计算，通过循环求得点集中的最近点对：

2）伪代码描述：

1
2
3
4
enumerate(const Point *test, int N)
	for i from 0 to N - 1
		for j from i + 1 to N
			ans = min(ans, dis(test[i], test[j]))

3）算法时间复杂度：算法一共要执行 $n(n-1)/2$次循环，因此算法复杂度为$O(n^2)$

2、分治法

1）算法描述：已知集合S中有n个点，分治法的思想就是将S进行拆分，分为两部分求最近点对。每次选择一条垂线L，将S拆分左右两部分为SL和SR，L一般取点集S中所有点的中间点的x坐标来划分，这样可以保证SL和SR中的点数目各为n/2

（否则以其他方式划分S，极端情况下可能会导致SL和SR中点数目一个为1，一个为n-1，不利于算法效率的准确性）

将左右两部分继续分解为更小的两部分，直到不能继续分解为止，用P1,P2来表示这两个部分，此时最终要求的最近距离可能在左边即P1中或者在右边即P2中，还有可能这个点对一个点在左边，一个点在右边

找出这两部分中的最小点对距离：d1和d2，记P1和P2中最小点对距离$d=min(d1，d2)$

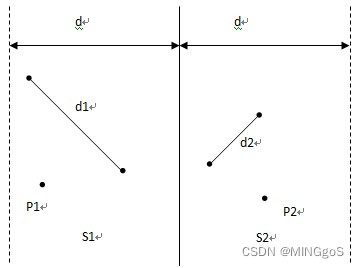
此时，P1中所有点与P2中所有点构成的点对均为最接近点对的候选者。在最坏情况下有$n/2$这样的候选者。

P1中任意一点p,它若与P2中的点q构成最接近点对的候选者，则必有$d(p,q)<d$。满足这个条件的P2中的点一定落在一个$d×2d$的矩形R中

由d的意义可知P2中任何2个S中的点的距离都不小于d，由此可以推出矩形R中最多只有6个S中的点。

将矩形R的长为$2δ$的边3等分，将它的长为$δ$的边2等分，由此导出6个$（d/2）×（2d/3）$的矩形。

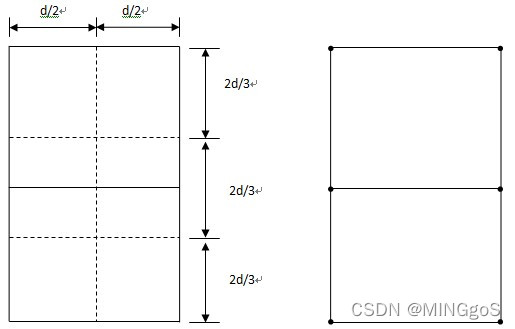
若矩形R中有多于6个S中的点，则由抽屉原理易知至少有一个$d×2d$的小矩形中有2个以上S中的点。设u,v是这样2个点，它们位于同一小矩形中，则这个小矩形中两点的最大距离即对角线的长度$sqrt((d/2)^2 + (2d/3)^2) = 5d/6 < d$

$d(u,v)≤5d/6 < d$。这与d的意义相矛盾。由反证法可以得出这个矩形R最多有6个点。

因此，在分治法的合并步骤中，我们最多只需要检查$6×n/2=3n$对候选者，而不是$n /2$个候选者。若将P1和P2中所有S的点按其y坐标排好序，则对P1中所有点p，对排好序的点列作一次扫描，就可以找出所有最接近点对的候选者，对P1中每一点最多只要检查P2中排好序的相继6个点。

由于分治算法的结构和归并排序的结构相类似，所以在合并的过程中采用归并排序的合并操作对候选点的y值进行排序，相当于一边递归一边排序，每次合并的排序开销为$O(n)$，因此算法整体的时间复杂度为$T(n)= 2T(n/2) + O(n)$，$T(n)= O(nlogn)$

2）伪代码描述：

1
2
3
4
5
6
7
merge(left, right)
	dist = INF;
	if(left == right) return dist;
		if(left + 1 == right) return 两点距离  
		mid = (left + right) / 2;
			dist1 = merge(left, mid), dist2 = merge(mid + 1, right);
			dist = min(dist1, dist2);
  1. 找出距离中点x坐标小于dist的点存入tmp数组
  2. 对tmp数组按y值进行归并排序的合并操作
  3. 对tmp数组中每个点遍历与它之后的6个点的距离更新最短距离

3）算法时间复杂度：

在分解前按照x值进行排序，时间复杂度为$O(n log n)$，合并阶段的开销时间复杂度为$O(n)$，递推式为

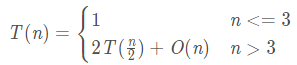
计算得出算法整体的时间复杂度为$O(n log n)$

三、算法测试结果及效率分析；

1.蛮力法

输入规模 处理时间 理论值
10000 0.57515 0.5751500
20000 2.30136 2.3006000
30000 5.19265 5.1763500
40000 9.21931 9.2024000
50000 14.8461 14.3787500
60000 21.5779 21.5779000
70000 29.0257 29.3699194
80000 38.1453 38.3607111
90000 48.4883 48.5502750
100000 59.7885 59.9386111

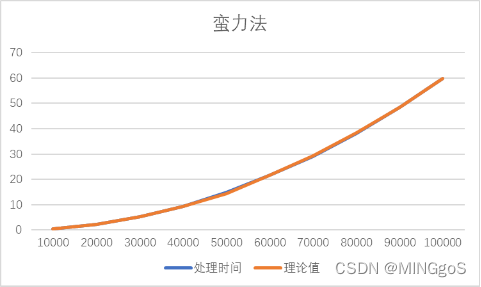
先选取输入规模n=10000的实际时间t1作为理论时间的基准。
当n=20000时，$t2=t1*(2/1)2$、
当n=30000时，$t3=t1*(3/1)2$，
以此类推做出表格数值，得出的理论值曲线基本与实际值曲线基本贴合。

2.分治法

100规模

输入规模 处理时间 理论值
100 7.06E-06 7.06E-06
200 1.77E-05 1.62E-05
300 2.68E-05 2.62E-05
400 3.57E-05 3.67E-05
500 4.65E-05 4.76E-05

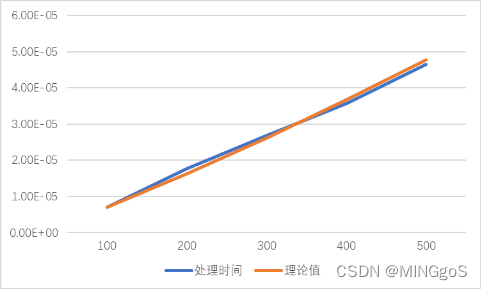
1000规模

输入规模 处理时间 理论值
1000 7.40E-05 7.40E-05
2000 0.00017 0.000163
3000 0.000267 0.000257
4000 0.000346 0.000355
5000 0.000436 0.000456

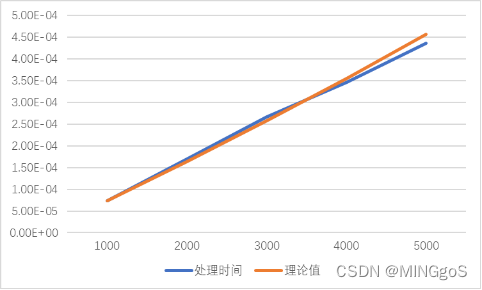
1w输入规模

输入规模 处理时间 理论值
10000 0.00089 8.90E-04
20000 0.001855 0.001913958
30000 0.002935 0.002988478
40000 0.003985 0.004095833
50000 0.0051 0.005227604

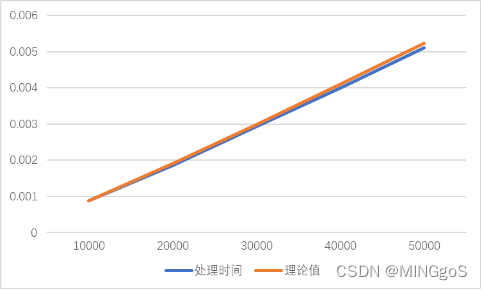
10w规模

输入规模 处理时间 理论值
100000 0.011 0.011
200000 0.0232 0.023324532
300000 0.0351 0.036149
400000 0.0494 0.049298128
500000 0.0615 0.06268867
600000 0.0753 0.076271597
700000 0.0887 0.09001451
800000 0.1012 0.103894384
900000 0.1154 0.117894002
1000000 0.1306 0.132

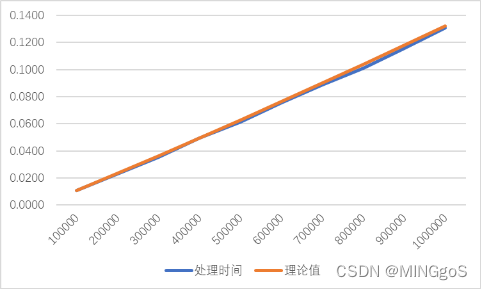
注：在代码实现的过程中采用了$O_3$优化，故算法运行时间稍快

O（nlog（n））复杂度时间推导

$tl=n1*log（2，n1）*t$， t1表示规模为n1的数据用时

$t2=n2*log（2，n2）*t$，t2表示规模为n2的数据用时

$t2=n2/n1*（log（2，n2）/1og（2，n1））*t1$

实际运行时间基本符合上述推导，每次合并的点都限制在$d*2d$的矩形之中，合并的开销稳定在$O(n)$，时间曲线较为稳定

误差分析：规模较小时，分治算法运行速度较快，而实现算法的代码采用的是time.h头文件的clock（）函数进行时间测量，会导致精度的丢失，所以在较小规模的测试中误差体现比较明显，只能将测试次数提高以降低误差，测试规模增大，算法运行时间明显趋于稳定

四．对求解这个问题的经验总结

  1. 在设计分治算法的过程中要尽可能地降低合并过程的开销，如果在以上设计的分治算法中对y值的排序直接采用快速排序进行排序的话，那么实际的合并代价为$O(n log n)$，而算法整体的时间复杂度则会退化成为$O（n log_2 n）$，并不是真正意义上的$O(n log n)$

  2. 在设计算法的过程中，可以利用蛮力求解的方式在小规模的数据验证算法的正确性

  3. 利用计算机的时钟作为种子产生的随机数来生成点的坐标会产生大量的重复，可以利用STL库中的set容器自己设置去重的规则进行去重，还可以获取cpu运行周期作为随机数产生的种子使得生成的随机数较为随机

  4. 灵活应用数学定理以辅助设计算法可以使得算法的时间复杂度获得极大的提升，如上面合并过程只需枚举6个点的证明过程，就使合并代价大大降低，数学工具是设计算法的利器