算法设计实验六
一、实验目的:
- 掌握最大流算法思想。
- 学会用最大流算法求解应用问题。
二、内容:
-
有m篇论文和n个评审,每篇论文需要安排a个评审,每个评审最多评b篇论文。请设计一个论文分配方案。
-
要求应用最大流解决上述问题,画出m=10,n=3的流网络图并解释说明流网络图与论文评审问题的关系。
-
编程实现所设计算法,计算a和b取不同值情况下的分配方案,如果没有可行方案则输出无解。
三、实验要求
-
在blackboard提交电子版实验报告,注意实验报告的书写,整体排版。
-
实验报告的实验步骤部分需详细给出算法思想与实现代码之间的关系解释,不可直接粘贴代码(直接粘贴代码者视为该部分内容缺失)。
-
实验报告中要求证明该算法的关键定理,并说明这些定理所起的作用。
-
实验报告样式可从http://192.168.2.3/guide.aspx 表格下载-学生适用-在校生管理-实践教学-实验:深圳大学学生实验报告)
-
源代码作为实验报告附件上传。
-
在实验课需要现场运行验证并讲解PPT。
四、问题分析
1.二分图的构建
将每一篇论文、每一位评审都抽象成为一个点,就可以得到一个论文的点集和一个评审的点集。如下左图(图1),数字从0到9的十个点的集合表示论文所属的点集,x,y,z三个点表示三位评审。

图 1 二分图的表示

图2 解决方案对应的二分图
如果一位评审评阅了这篇论文,那么我们就在这位评审和这篇论文对应的点之间连接一条边。在这个二分图中一条边表示一篇论文和一个评审的匹配。
假定每篇论文需要一位评审,每个评审最多评审4篇论文,那么我们可以得到x评审0到3号四篇论文,y评审4到7号四篇论文,z评审8,9号论文这样一种解决方案,那么画出这个解决方案的二分图就可以得到上方右图(图2)这样的一个二分图。
2.流网络的搭建
①虚拟源点和汇点
要使用最大流算法解决论文评审方案分配的问题,我们首先需要有一个流网络,目前已经有了一个二分图,搭建流网络我们还需要一个源点和一个汇点。
如下图,我们分别在论文点集的左边虚拟了一个源点S ,在评审点集的右边虚拟了一个汇点T。
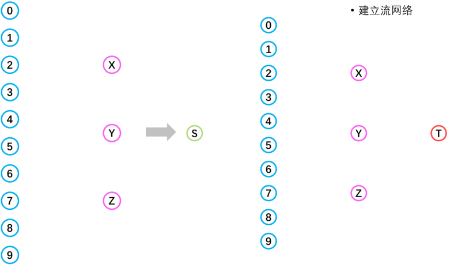
图 3 虚拟源点、 汇点
②容量设置
对于一篇论文,它需要安排a位评审,所以源点和每一个论文对应的点之间的边容量上限应该设置为a,如果小于这个值那么流网络无法输出解决方案。
对于一位评审,他最多能评b篇论文,所以评审对应的点连接到汇点的边容量上限应设置为b。
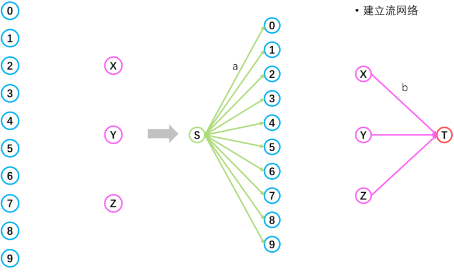
图 4 容量限制
论文和评审之间的边的容量应该都设置为1,一个评审不会多次评阅相同的一篇论文,而相同的一篇论文可以被所有的评审进行评阅,所以一个论文点会和所有的评审有边连接的关系,而这些边的容量为1,如果一条边的流量为1就说明这条边对应的评审评阅了这篇论文,
为0则没有评阅。
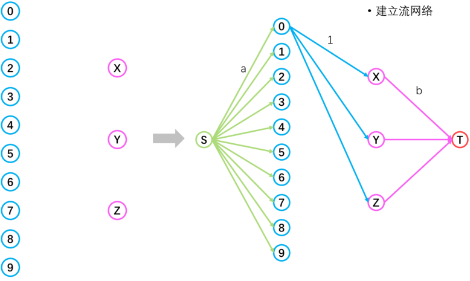
图 5 论文与评审之间边的容量限制。
对所有的论文和评审进行连接并设置容量限制,得到下图中的流网络。
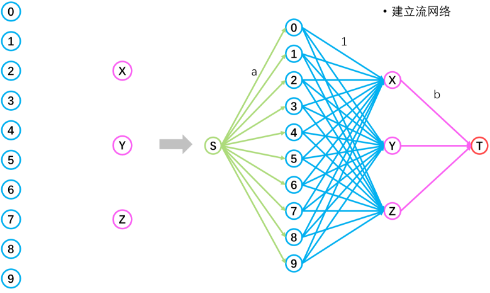
图 6 完整的流网络图
③正确性证明
要对一个二分图使用最大流算法,我们只需要证明对于二分图的解空间中的任意一个可行解一定可以在流网络中找到一个对应的可行流,在流网络中的任意一个可行流一定可以在二分图的解空间中找到一个对应的可行解,这样解空间中的最大匹配就对应于流网络中的最大流
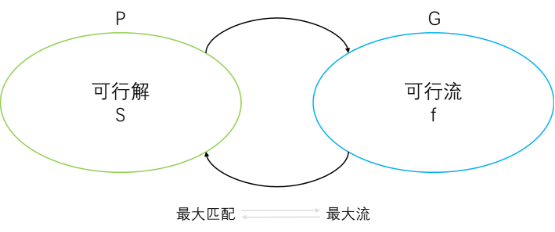
(1)二分图中的任意匹配一定可以在流网络中找到一个对应的可行流。如下图,对于左边的二分图,其对应于右边的流网络,网络中的流量满足容量限制和流量守恒,所以这个流量是合法的可行流。
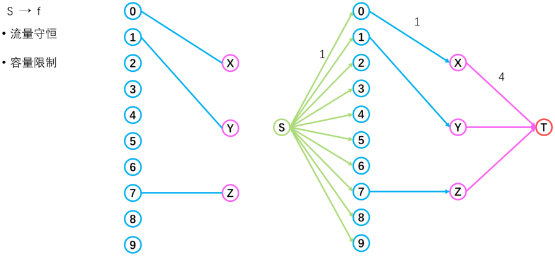
图 8 可行解对应于可行流
(2)流网络中的任意一个可行流一定可以在二分图中找到一个对应的匹配关系,流网络中的每一个流量的数值大小都是整数值,而对于两个点集之间有流量的边,单独拿出来就是对应二分图匹配关系。如下图,由于流量值都是整数,并且中间的边流量要么是零要么是一,只有这两个数可行,所以左边的流网络课以对应于右边的二分图。
图 9 可行流对应于可行解
由此,我们可以说明二分图解空间的最大解对应于流网络的最大流,所以我们可以使用最大流算法求解二分图的匹配方案。
3.是否存在可行的匹配方案
①每篇论文需要的评审数量要少于或等于评审的人数即$a ≤ n$
②论文需要的评审总次数小于等于评审们最多能评审的数量即 $a × m ≤ b × n$
满足上面两条不等式则说明存在可行的匹配方案,否则不存在可行的匹配方案
五、算法原理描述
1.FF方法
(1)算法思想
只要有一条从源点(开始节点)到汇点(结束节点)的路径,在路径的所有边上都有可用容量,就沿着这条路径发送一个流,流量由路径上的最小容量限制。 然后再找到另一条路径,一直到网络中不存在这种路径为止。 一条有可用容量的路径被称为一条增广路径。
算法过程如下所示
①路径$S -> 1 -> 3 -> T$ 为一条增广路径,最小容量为2,向这条路径发送流量值为2的流量。
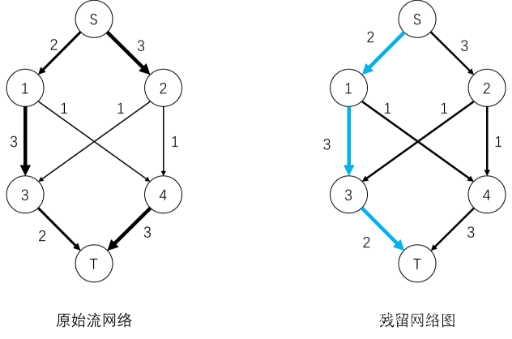
②路径$S -> 2 -> 4 -> T$ 为一条增广路径

③ 增广路径$S -> 2 -> 3 -> 1 -> 4 -> T$
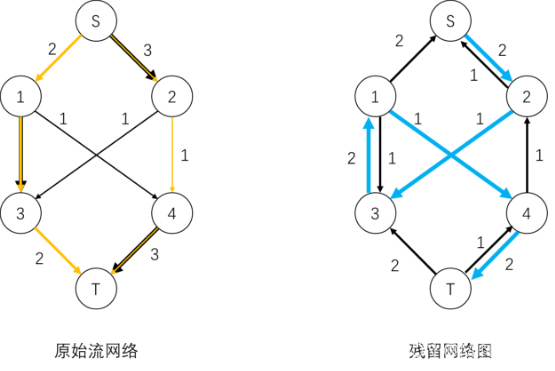
④再无增广路径,发送出去的流量值之和为最大流

(2)最坏情况分析
存在某些特殊的边可能会导致算法效率降低,如下图,有可能先找到增广路径$S->2->1->T$,然后找到增广路径$S->1->2->T$,接着增广$S->2->1->T$,依次重复增广两百万次才完成对这个流网络的增广。
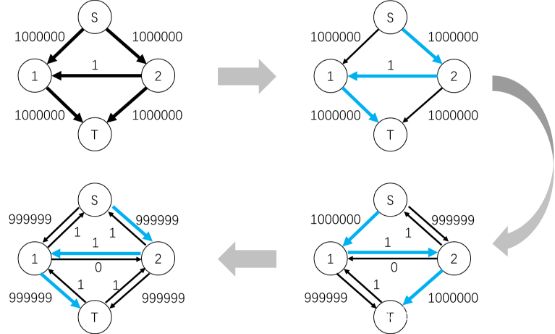
(3)伪代码描述

(4)算法时间复杂度
找到一条增广路径的时间复杂度为$O(E)$,有上述最坏情况分析可得,算法整体的时间复杂度为$O( E |f*| )$,其中, $|f*|$为最大流,$E$为边数
2.EK算法
(1)算法思想
采用BFS的方式搜索增广路径来实现FF方法,可以确保每次找到的增广路径都是长度最短的路径,如上述FF方法的最坏情况,使用BFS的搜索方式则只需要搜索两条增广路径就能结束算法。如下图,算法增广完$S -> 2 -> 1 -> T$和$S -> 1 -> 2->T$这两条路径就结束。

(2)伪代码描述

(3)算法时间复杂度
查阅资料得EK算法的时间复杂度为$O(V E^2)$,其中, $V$为点数,$E$为边数
3.Dinic算法
(1)算法思想
Dinic 算法 的过程是这样的:每次增广前,我们先用 BFS 来将图分层。设源点的层数为0,那么一个点的层数便是它离源点的最近距离。
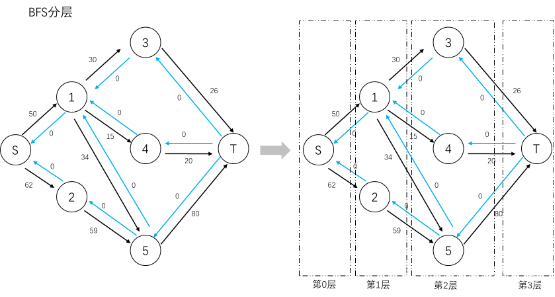
图 17
通过BFS分层,我们可以寻找是否存在增广路径,并确保找到的增广路径是最短路径。
我们每次找增广路的时候,都只找比当前点层数多 1的点进行增广(这样就可以确保我们找到的增广路是最短的),即DFS搜索。
如下图,1、2、3三个点形成环,如果使用FF方法,那么就有可能会在这环上不断绕圈,而采用BFS分层,并严格按照层数多1的方式搜索路径,则会避免这种情况。

如图17,我们对流网络分层完之后可以找到如图18左侧的一条增广路径,对其进行增广,得到右侧的残留网络,很明显,这个分层图依旧存在增广路径。如果是EK算法,则在这个时候会重新遍历整个流网络搜索增广路径,而Dinic算法采用dfs的方式在这个基础之上搜索增广路径,如图19至图21所示,最后得到图21右侧没有增广路径的残留网络,才会重新使用BFS对流网络重新分层以寻找增广路径。
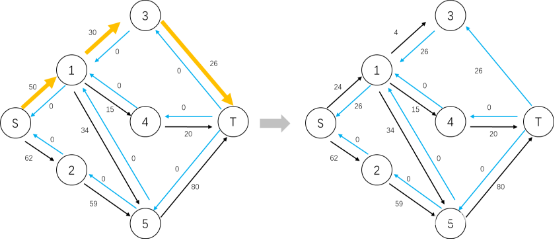
图 18
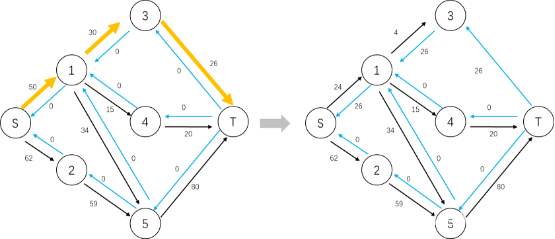
图 19

图 20
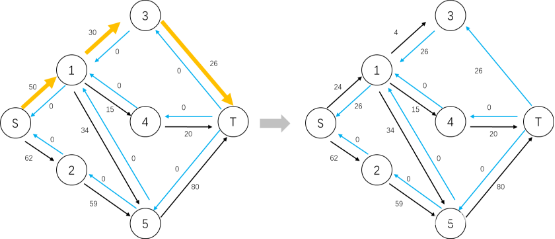
图 21
(2)算法优化
①多路增广
每次找到一条增广路的时候,如果残余流量没有用完的话,我们就可以利用残余部分流量,再找出一条增广路。这样就可以在一次 DFS 中找出多条增广路,大大提高了算法的效率。
如下图22,对于S发送到1号点的流量50份单位流量,然后对路径$1 -> 3 -> T$进行增广,之后1号点还剩下24份流量,接着对路径$1 -> 4 -> T$进行增广,1号点还剩下9份流量,再将剩余的流量发送到$1 -> 5 -> T$这条路径上,这样一次DFS就实现了对多条路径的增广。

②废点优化
对于一个点,如果所有流入他的边都已经饱和了,那么之后的增广过程中一定不会再用到这个点,将这个点废弃掉,层数设置为-1,就不会再次搜索到这个点了。
如下图,在多路增广的过程中,流入点1的所有边的流量都已经饱和了,将1号点的层数设置为-1,本次BFS构建出来的分层图不再搜索1号点。
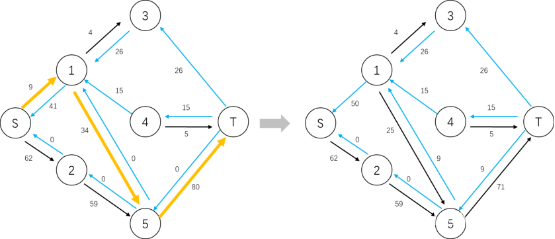
③当前弧优化
如果一条边已经被增广过并且达到饱和,那么它就没有可能被增广第二次。那么,我们下一次进行增广的时候,就可以不必再走那些已经被增广过的边。
如下图,假定这个网络首先增广路径2 ~ k – a 和2 ~ k – b并且k - a和k - b这两条边达到饱和,那么在增广路径1 ~ k 的时候,不再需要考虑k - a和k - b这两条边,只需要从k - c这条边开始增广。
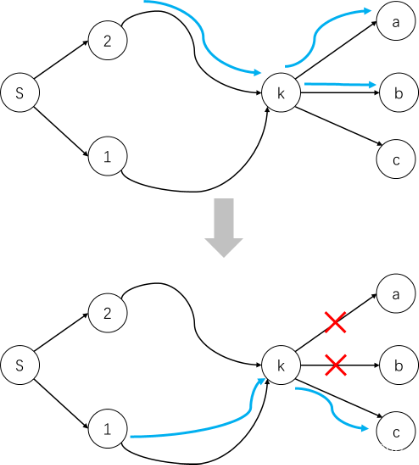
(3)伪代码描述



(4)算法时间复杂度
每轮BFS搭建分层图找到的增广路的数量至少为1,增广路的数量每次都减少至少一条, 整个网络中最多有n - 1条增广路, n顶点数量。分层图可以在$O(E)$的时间复杂度内用BFS构建。一条增广路可以在$O(VE)$的复杂度内构建。Dinic算法整体的时间复杂度为$O(V^2E)$
3.预流推进
上面提及的算法都是增广路算法,即按照增广路径不断压入少量的流量,直到满流,而预流推进算法则是一次性将巨额流量压入网络,如果能够流就让他流,即将流量转到下一个节点,否则就溢出,不管溢出的部分。可以推送流量就推送流量,最终汇点T有多少流量就是最大流。
- 基本概念
- 余流:每个点当前有多少水。
- 推流:把该点的余流推给周围点
- 高度:流网络中的每个点都有一个高度,水只会从高处往低处流,算法只会在$h(u)= h(v)+ 1$的边$(u,v)$执行推流
- 溢出:超额流$eu= (x,u)∈Efx,u- (u,y)∈Ef(u,y) > 0,$则称结点u溢出
- 重贴标签(Relabel):如果节点u溢出,且$∀(u,v)∈Ef, h(u)<=h(v)$ 则u点适合使用relabel操作,将$h(u)$更新为 $minhv+1,(u,v)∈Ef$即可
(2)算法思想
1.先假装s有无限多的水(余流),从s向周围点推流(把该点的余流推给周围点),并让周围点入队
2.不断地取队首元素,对队首元素推流
3.队列为空时结束算法,t点的余流即为最大流。
注意事项
①在开始预流推进前要先把S的高度改为n(点数),避免一开始S推流过去的点就直接把余流倒流回S。
②S和T不能进入队列
③推的流量不能超过边的容量也不能超过该点余流
④如果$(u,v)$在推流完之后满流,则将这条边在残留网络中删除。
(3)算法过程
对于下面的流网络,我们使用红色数字表示余流,蓝色数字表示高度。荧光底色标记着发生变化的数值
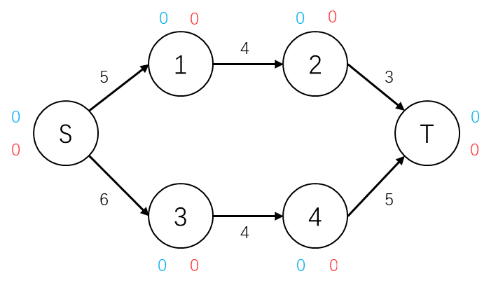
首先,网络中有六个点,先将源点S的高度设置为6,然后向与源点连接的点推送流量,源点的余流为-11,1号点的余流为5,3号点的余流为6,(S,1)和(S,2)的边权设置为0。
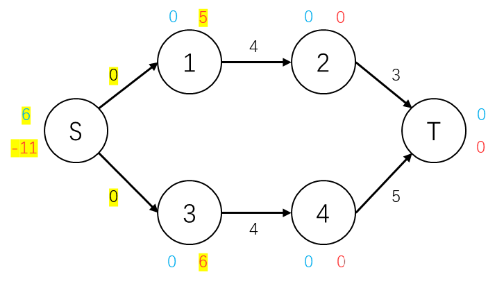
此时,1号点,3号点有余流,将他们的高度抬高。
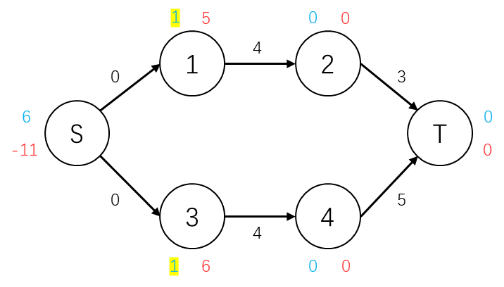
对1号点执行推流操作
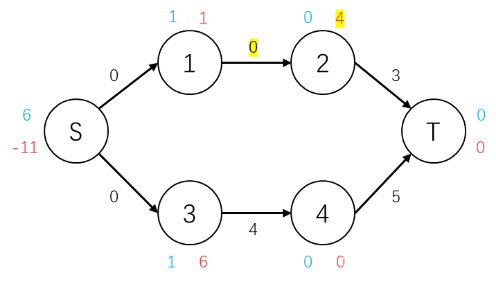
与1号点连接的边都达到饱和状态,不能继续执行推流操作,继续抬高1号点的高度
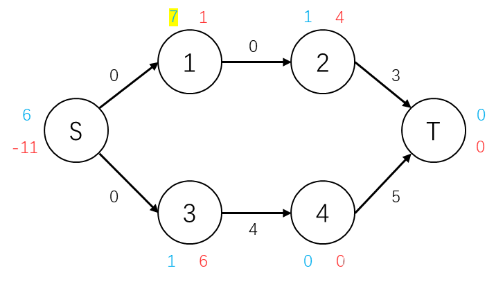
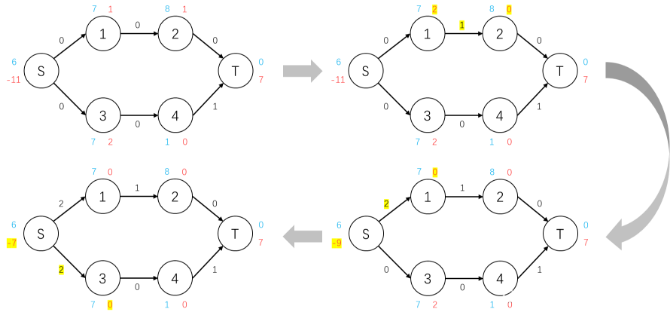
依此类推,不断地对流网络中的点执行推流,然后重新设置高度,直到整个网络中除了源点和汇点其他的点都没有余流,那么这个时候汇点中的流量值就是最大流的流量值

(4)算法优化
① 堆优化
最高标号预流推进算法(High Level Preflow Push)简称HLPP
是基于预流推进算法的优先队列实现,该算法优先推送高度高的溢出的结点。
具体地说,HLPP 算法过程如下:
1.初始化(基于预流推进算法);
2.选择溢出结点(除 S,T)中高度最高的结点u,并对它所有可以推送的边进行推送;
3.如果 u仍溢出,对它重贴标签,回到步骤 2;
4.如果没有溢出的结点,算法结束。
②BFS优化
在初始化高度的时候进行优化。具体来说,我们初始化 h(u)为u到t的最短距离;特别的,h(s) = n(n为顶点数)。在 BFS 的同时我们可以顺带地检查图的连通性,排除无解的情况。
如下图,通过从汇点T 开始BFS整个流网络可以得到右边节点带有高度的流网络

③GAP优化
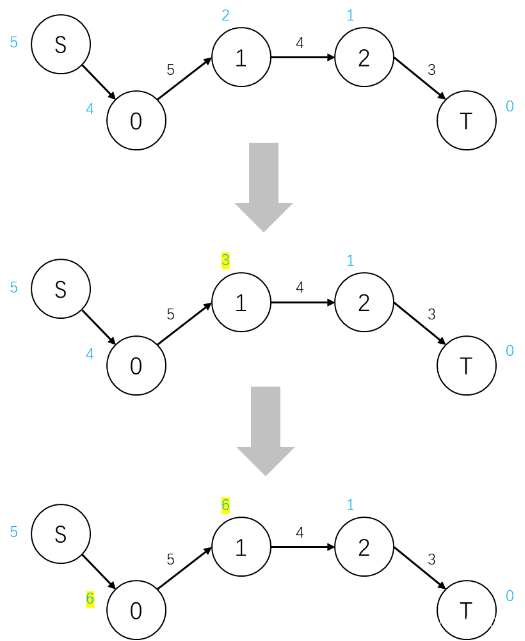
HLPP 推送的条件是h(u)= h(v)+ 1,而如果在算法的某一时刻,h(u) = k的结点个数为0,那么对于h(u) > k的结点就永远无法推送超额流到汇点T,因此只能送回源点S,那么我们就在这时直接让他们的高度变成n + 1,以尽快推送回源点S,减少重贴标签的操作。
如下图,算法在某个时刻将1号点的高度从2抬高到3,然后发现图中高度为2的节点数量为0,那么我们将0号点和1号点的高度设置为6,以使得它们的余流加快回流到源点S
(5)伪代码描述




(3)算法时间复杂度
查阅资料得EK算法的时间复杂度为 $O(V^2E^{1/2})$,其中, V为点数,E为边数
六、效率分析(时间单位:us)
由于最大流算法的时间复杂度上界比较宽松,并且本实验的流网络结构较为简单且层数固定,因此不作理论效率的比较,只通过不同参数的变化分析时间效率的变化;
1.其他值固定,改变a的值
时间单位:ms
| a | EK | Dinic | HLPP |
|---|---|---|---|
| 5 | 1308.17 | 5.0402 | 15.636 |
| 10 | 3794.81 | 3.145 | 27.5953 |
| 15 | 7434.1 | 4.1857 | 46.3086 |
| 20 | 12774.3 | 4.7355 | 74.1043 |
| 25 | 20119.8 | 5.168 | 96.5127 |
b = 25, n = 500, m = 500
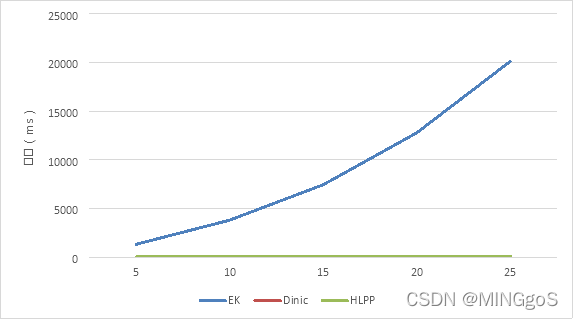
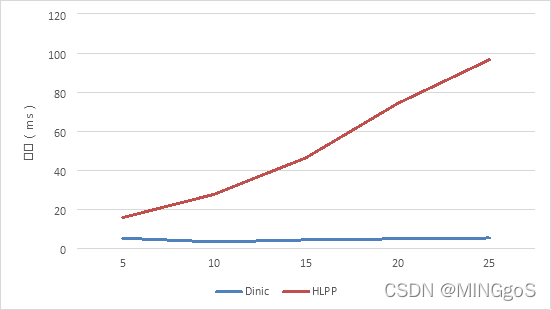
a增大,EK和HLPP需要遍历的边和点数量增大,EK,HLPP 所需时间增多
对 Dinic 的效率影响不大
- 其他值固定,改变b的值
时间单位:ms
| b | EK | Dinic | HLPP |
|---|---|---|---|
| 5 | 4776.69 | 6.1278 | 100.655 |
| 10 | 2228.4 | 2.748 | 36.1762 |
| 15 | 1754.15 | 2.7448 | 22.0881 |
| 20 | 1471.36 | 2.2022 | 16.2429 |
| 25 | 1301.78 | 2.5006 | 14.6073 |
a = 5, n = 500, m = 500
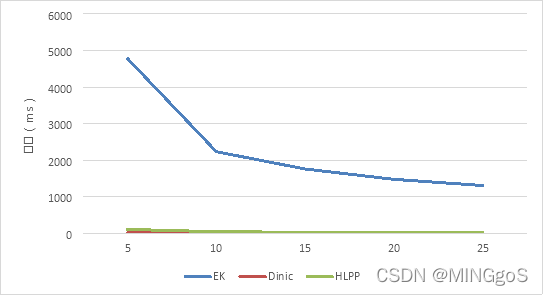
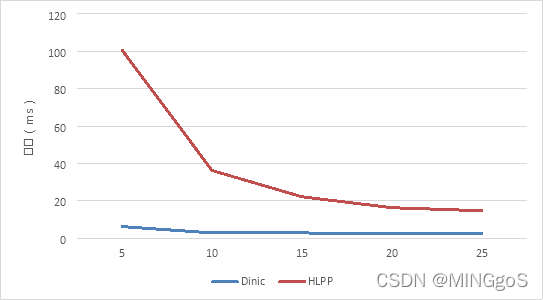
b增大,增广路径随b的增大而增加,EK,HLPP 所需时间减少
对 Dinic 的效率影响不大
- 其他值固定,改变n的值
时间单位:ms
| n | EK | Dinic | HLPP |
|---|---|---|---|
| 100 | 599.6 | 2.4803 | 8.6507 |
| 200 | 765.851 | 1.5216 | 9.8194 |
| 300 | 945.658 | 1.6449 | 12.229 |
| 400 | 1081.43 | 2.2724 | 13.2294 |
| 500 | 1290.19 | 2.9115 | 14.4041 |
a = 5, b = 25, m = 500
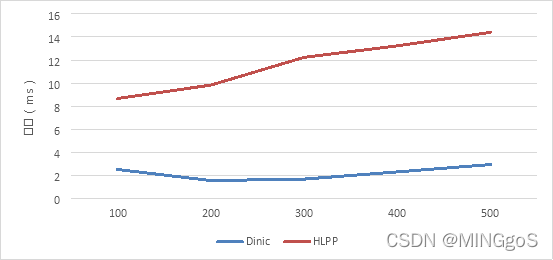

n增大,增广路数量增大,EK,HLPP 所需时间增大
对 Dinic 的效率影响不大
\4. 其他值固定,改变m的值
时间单位:ms
| m | EK | Dinic | HLPP |
|---|---|---|---|
| 100 | 43.856 | 1.7683 | 4.1706 |
| 200 | 160.41 | 1.1502 | 3.8335 |
| 300 | 407.002 | 1.2255 | 6.5871 |
| 400 | 783.97 | 1.7507 | 10.0239 |
| 500 | 1382.34 | 2.0253 | 13.4699 |
a = 25, b = 25, n = 500
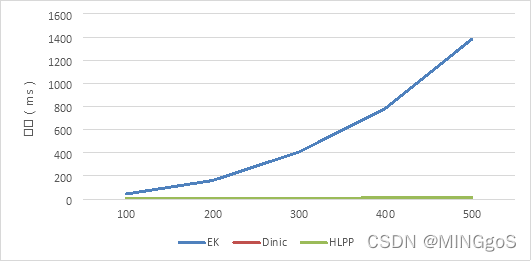
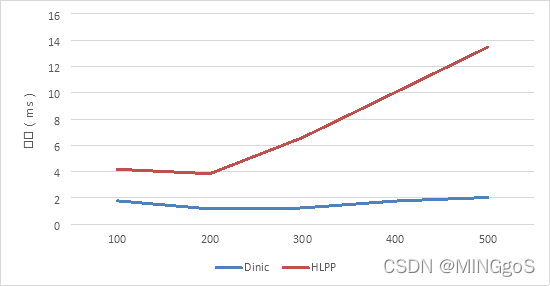
m增大,增广路数量增大,EK,HLPP 所需时间增大
对 Dinic的效率影响不大
在上面的数据测试中,可以发现本实验的几种最大流算法中Dinic算法的表现最为优异,主要原因是Dinic算法的多路增广在这个实验构建的流网络效果最佳,以及Dinic实际上只需要在这个网络中使用一次BFS构建分层图就可以多次进行多路增广,所以即便Dinic的时间复杂度为$O(V^2E)$依旧表现优异。
EK算法则是由于每次寻找增广路都需要进行一次BFS搜索,并且论文点集和评审点集之间的边相对来说比较稠密,所以相同规模的图EK算法在这三个算法之中效率最低。
再看时间复杂度为$O(V^2E^{1/2})$的HLPP算法,HLPP算法的时间复杂度在这个三个算法中最低,但是其他算法的时间复杂上界较为宽松,而HLPP算法实际运行是比较贴近它自身的时间复杂度的。由于本实验的流网络结构比较简单,而且层数只有四层,所以HLPP的各种优化在计算最大流的优势反而在这个实验之中体现不出来,并且对应的操作带来的时间消耗使得HLPP在这个流网络中的各项效率均差于Dinic算法。
七、实验心得
- 网络流算法的普遍化及专门化
我们可以利用网络流去找出最大流是最简单及最普通的问题,它提供了在一指定的图中由源点到汇点的最大可能总流量。还有很多其它问题可以利用最大流算法去解决,假设它们可以适当地塑造成流网络的模样,例如二分图匹配(Bipartite Matching)、任务分配问题(Assignment Problem)和运输问题(Transportation Problem)。
- 流网络的建立
如果我们能找到问题的解空间中可行解和流网络中可行流之间一一对应的关系,那我们就可以使用最大流算法来求解问题的最大可行解